一次刷题

其实这篇文章主要是为了记录一下关于桶排序的，然后顺便也记录一下其他的排序算法。

说到桶排序还是因为有一次做一 acm 题，主要是对一堆数进行排序。当时觉得水题。。水题。。水水更健康，单身 20 年手速撸完一发冒泡，直接返回了个Time Limit Exceeded.

后来看了一下题解，发现很多人用Pascal写了桶排序 AC 了，当时也没看过关于桶排序，前段时间看了些资料，然后简单记录一下它的思想。

描述

计算 x^n 常见的算法就是使用 n-1 次乘法自乘，更高效的做法我们可以使用递归。以乘法的次数来作为运行时间的度量，下面是两种算法的比较。

算法 2 的数学原理:

• 若 n 为偶数X^n = X^(n/2) * X^(n/2).
• 若 n 为基数X^n = X^[(n-1)/2] * X^[(n-1)/2] * X.

算法简述

欧几里德算法又称辗转相除法，用于计算两个正整数 a，b 的最大公约数。定理：两个整数的最大公约数等于其中较小的那个数和两数的相除余数的最大公约数。最大公约数gcd(greatest common divisor)

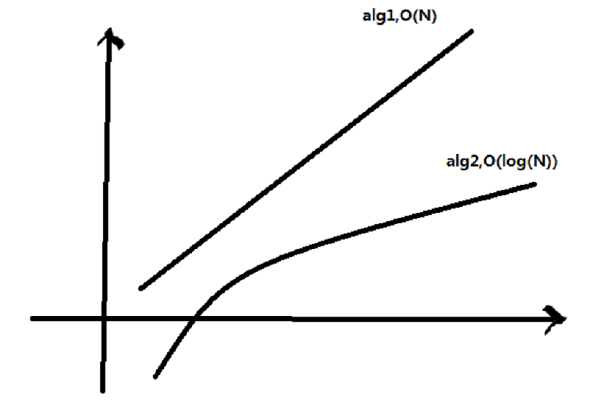
求最大公约数常规的方法就是从 M，N(M>N)反向 N 循环与 M，N 进行取模运算，得到最大数，下面的方法时间复杂度为 O(logN)会更高效。

也可以看看hsfzxjy同学的证明过程https://segmentfault.com/q/1010000004427096

数学基础

定义

• 如果存在正常数 c 和 n，使得当 N>=n 时，T(N)<=cf(N)，则记为 T(N)=O(f(n))。
• 如果存在正常数 c 和 n，使得当 N<=n 时，T(N)>=cg(N)，则记为 T(N)=Ω(g(n))。

如果我们用传统的不等式来计算增长率，那么第一个定义就是说 T(n)的增长率小于 f(n)的增长率。第二个定义 T(N)=Ω(g(n))意思就是 T(N)的增长率大于 g(n)的增长率。

当我们说 T(N)=O(f(n))时，我们是在保证函数 T(N)在不快于 f(N)的速度增长；因此说 T(N)是 f(N)的一个上界(upper bound)，与此同时说 T(N)是 f(N)的一个下界(lower bound)。好比说 N^3 增长比 N^2 快，因此我们可以说是 N^2=O(N^3)或者 N^3=Ω(N^2)。

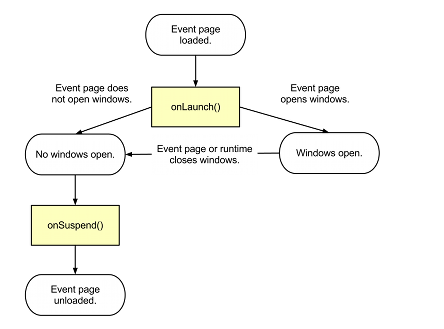
chrome.storage

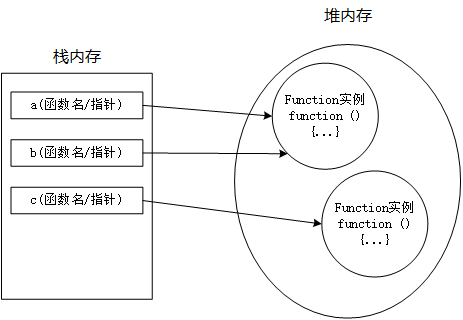
DOM 介绍

DOM(Document Object Model) 文档对象模型，是针对 HTML 和 XML 文档的一个 API。DOM 描绘了一个层次化的节点树，允许开发人员添加、修改、删除页面中的某一部分。DOM 脱胎于 Netscape 以及 Microsoft 创始的 DHTML(动态 HTML)，但它现在已经成为表现和操作页面标记的真正的跨平台、语言中立的方式。

注意，IE 中所有 DOM 对象都是以 COM 对象的形式实现的。这意味着 IE 中的 DOM 对象与原生 Javascript 对象的行为或活动特点并不一致。

W3C DOM 标准

• Core DOM 针对任何结构化文档的标准模型。
• XML DOM 针对 XML 文档的标准模型。
• HTML DOM 针对 HTML 文档的标准模型。

Function 类型

在 ECMAScript 中函数实际上是对象，每个函数都是 Function 类型的实例，且与其他引用类型一样具有属性和方法，由于函数的本质是对象，那么函数名应该是指向对象的指针。一个对象可以有多个引用，所以一个函数可以有多个函数名(指针)。函数的参数也不是必要的（有 arguments 对象），也没有函数签名的说法，这也是为什么 js 的函数不能重载。

Chrome Apps 紧密结合与用户的操作系统.设计他们的目的是为了作为一个单独的 Tab 独立于浏览器运行,在离线环境或则在网络连接性很差的情况下比起经典的 web 环境中还能具有强大的功能. 应用程序容器、编程和安全模型都满足这些 Chrome 应用程序的需求。

App 容器模型

应用程序容器描述了 Chrome 应用程序的视觉外观和加载行为. Chrome Apps 与传统的 web 页面看起来不一样是因为 app 容器不显示任何传统网页中的 UI 控件.它只显示一个矩形的空白区域, 这允许应用程序融合与“本地”系统上的应用程序, 而且可以防止用户通过手动更改程序的 URL 地址来混乱 App 的逻辑.

如果你不熟悉内容安全策略 CSP(Content Security Policy), 这里有一个关于 CSP 的介绍, 该文档覆盖更为广泛的网络平台对 CSP 的看法. Chrome App 的内容安全策略不是那么的灵活, 你也应该阅读Chrome 扩展应用的内容安全策略, 它是作为 Chrome App 内容安全策略的基础. 为了简洁起见,我们在这里不要重复相同的信息.

CSP 是一种为了减轻跨站点脚本的安全策略, 我们都知道, 跨站点脚本是不好的. 我们不会试图说服你, CSP 是一个温暖而舒适的新的策略. 涉及的工作: 你需要学习如何使用不同的方式来做基本任务.

本文档的目的是为了告诉你什么是 Chrome App 中的 CSP. 你该如何的去遵守他, 以及你可以通过遵守 CSP 来完成基本的任务.

这篇文章可能不完整

好吧最近撸码撸得想吐，什么都不想干了，抽点时间写写博客。以下是之前在 libGDX 学习中遇到的一些关于 Mesh 问题。关于 Mesh (图元)在 libgdx 中的使用，本来对于国内 libgdx 的开发资料比较缺乏，之前也看了网上的一些教程，感觉很对都没有写清楚（还是我理解能力太差？）或者是把它讲得比较复杂，难以理解。浏览了部分资料后自己写了一个 demo。 本文采用 libGDX-0.99 版本，1.x 版本 API 可能会有变化。

API

qute: A Mesh consists of vertices and optionally indices which specify which vertices define a triangle. Each vertex is composed of attributes such as position, normal, color or texture coordinate. Note that not all of this attributes must be given, except for position which is non-optional. Each attribute has an alias which is used when rendering a Mesh in OpenGL ES 2.0. The alias is used to bind a specific vertex attribute to a shader attribute. The shader source and the alias of the attribute must match exactly for this to work.

大致说明了一个 mesh 包含了多个 vertice 即顶点，每个顶点都有各自的属性，包括颜色、位置、纹理等等。平时常用的构造函数就是: